Keeps and breaks

The layout galleys and the layout tree which is their context have been discussed elsewhere. Here we discuss a possible method of implementing keeps and breaks within the context of layout galleys and the layout tree.

Breaks

Breaks may be handled by inserting a column- or page-break pseudo-object into the galley stream. For break-before, the object would be inserted before the area in which the flow object, to which the property is attached, is leading. If the flow object is leading in no ancestor context, the pseudo-object is inserted before the object itself. Corresponding considerations apply for break-after. Selection of the position for these objects will be further examined in the discussion on keeps.

Keeps

Conceptually, all keeps can be represented by a keep-together pseudo-area. The keep-together property itself is expressed during layout by wrapping all of the generated areas in a keep-together area. Keep-with-previous on formatting object A becomes a keep-together area spanning the first non-blank normal area leaf node, L, generated by A or its offspring, and the last non-blank normal area leaf node preceding L in the area tree. Likewise, keep-with-next on formatting object A becomes a keep-together area spanning the last non-blank normal area leaf node, L, generated by A or its offspring, and the first non-blank normal area leaf node following L in the area tree.
TODO REWORK THIS for block vs inline

The obvious problem with this arrangement is that the keep-together area violate the hierarachical arrangement of the layout tree. They form a concurrent structure focussed on the leaf nodes. This seems to be the essential problem of handling keep-with-(previous/next); that it cuts across the otherwise tree-structured flow of processing. Such problems are endemic in page layout.

In any case, it seems that the relationships between areas that are of interest in keep processing need some form of direct expression, parallel to the layout tree itself. Restricting ourselves too block-level elements, and looking only at the simple block stacking cases, we get a diagram like the attached PNG. In order to track the relationships through the tree, we need four sets of links.

Figure 1

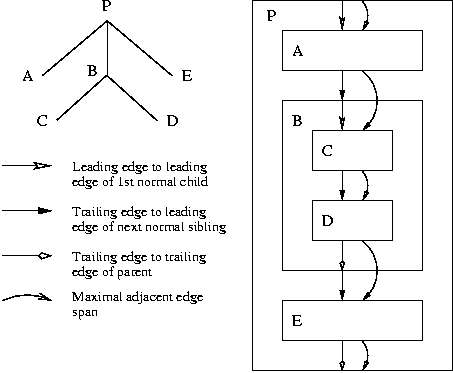
The three basic links are:

• Leading edge to leading edge of first normal child.
• Trailing edge to leading edge of next normal sibling.
• Trailing edge to trailing edge of parent.

Superimposed on the basic links are bridging links which span adjacent sets of links. These spanning links are the tree violators, and give direct access to the areas which are of interest in keep processing. They could be implemented as double-linked lists, either within the layout tree nodes or as separate structures. Gaps in the spanning links are joined by simply reproducing the single links, as in the diagram. The whole layout tree for a page is effectively threaded in order of interest, as far as keeps are concerned.

The bonus of this structure is that it looks like a superset of the stacking constraints. It gives direct access to all sets of adjacent edges and sets of edges whose space specifiers need to be resolved. Fences can be easily enough detected during the process of space resolution.